CBT No.2 Lic. Carlos Pichardo
Química: Modelo atómico de Schrödinger
Integrantes:
Moreno Castellanos Wendy Guadalupe
VillaFuerte Morales Lourdes Sarahi
VillaSeñor Galindo Enrique
Martinez Maldonado Emilio Rodrigo
Perez Beltran Nelly Berenice
Salazar Sarabia Diana Lizet
Grado:2º Grupo:210 Instrumentación Dental
PROFESORA: Gabriela Ramirez Sanchez
Modelo Atómico De Schrödinger
(1924) es un modelo cuántico no relativista. Se basa en la solución de la ecuación de Schrödinger para un potencial electrostático con simetría esférica, llamado también átomo hidrogenoide. En este modelo los electrones se contemplaban originalmente como una onda estacionaria de materia cuya amplitud decaía rápidamente al sobrepasar el radio atómico.
El modelo de Bohr funcionaba muy bien para el átomo de hidrógeno. En los espectros realizados para otros átomos se observaba que electrones de un mismo nivel energético tenían energías ligeramente diferentes. Esto no tenía explicación en el modelo de Bohr, y sugería que se necesitaba alguna corrección. La propuesta fue que dentro de un mismo nivel energético existían subniveles. La forma concreta en que surgieron de manera natural estos subniveles, fue incorporando órbitas elípticas y correcciones relativistas. Así, en 1916, Arnold Sommerfeld modificó el modelo atómico de Bohr, en el cual los electrones solo giraban en órbitas circulares, al decir que también podían girar en órbitas elípticas más complejas y calculó los efectos relativistas.
CARACTERÍSTICAS DEL MODELO
El modelo atómico de Schrödinger concebía originalmente los electrones como ondas de materia. Así la ecuación se interpretaba como la ecuación ondulatoria que describía la evolución en el tiempo y el espacio de dicha onda material. Más tarde Max Born propuso una interpretación probabilística de la función de onda de los electrones. Esa nueva interpretación es compatible con los electrones concebidos como partículas cuasipuntuales cuya probabilidad de presencia en una determinada región viene dada por la integral del cuadrado de la función de onda en una región. Es decir, en la interpretación posterior del modelo, este era modelo probabilista que permitía hacer predicciones empíricas, pero en el que la posición y la cantidad de movimiento no pueden conocerse simultáneamente, por el principio de incertidumbre. Así mismo el resultado de ciertas mediciones no están determinadas por el modelo, sino solo el conjunto de resultados posibles y su distribución de probabilidad.
SOLUCIÓN DE LA ECUACIÓN Schrödinger
Las soluciones estacionarias de la ecuación de Schrödinger en un campo central electrostático, están caracterizadas por tres números cuánticos (n, l, m) que a su vez están relacionados con lo que en el caso clásico corresponderían a las tres integrales del movimiento independientes de una partícula en un campo central. Estas soluciones o funciones de onda normalizadasvienen dadas en coordenadas esféricas por:
![\psi_{nlm}(\theta,\phi,r) = \langle \vec r|nlm\rangle = \sqrt {{\left ( \frac{2}{n a_0} \right )}^3\frac{(n-l-1)!}{2n[(n+l)!]}2} e^{-{r \over {na_0}}}\left({2r \over {na_0}}\right)^l L_{n-l-1}^{2l+1}\left[{2r \over {na_0}}\right] Y_{l,m}(\theta, \phi )](https://upload.wikimedia.org/math/3/3/e/33e4c3a3a89407fe785941834eb35c67.png)
donde:
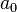 es el radio de Bohr.
es el radio de Bohr. son los polinomios generalizados de Laguerre de grado n-l-1.
son los polinomios generalizados de Laguerre de grado n-l-1. es el armónico esférico (l, m).
es el armónico esférico (l, m).
Los autovalores son:
Para el operador momento angular:


Para el operador hamiltoniano:

- donde:

- α es la constante de estructura fina con Z=1.
Insuficiencias del modelo
- Si bien el modelo de Schrödinger describe adecuadamente la estructura electrónica de los átomos, resulta incompleto en otros aspectos:
- El modelo de Schrödinger en su formulación original no tiene en cuenta el espín de los electrones, esta deficiencia es corregida por el modelo de Schrödinger-Pauli.
- El modelo de Schrödinger ignora los efectos relativistas de los electrones rápidos, esta deficiencia es corregida por la ecuación de Dirac que además incorpora la descripción del espín electrónico.
- El modelo de Schrödinger si bien predice razonablemente bien los niveles energéticos, por sí mismo no explica por qué un electrón en un estado cuántico excitado decae hacia un nivel inferior si existe alguno libre. Esto fue explicado por primera vez por la electrodinámica cuántica y es un efecto de la energía del punto cero del vacío cuántico.
Cuando se considera un átomo de hidrógeno los dos primeros aspectos pueden corregirse añadiendo términos correctivos al hamiltoniano atómico. - En conclusión, el modelo de Schrödinger, nos hace abandonar por completo el concepto anterior de los electrones, que venían definidos como pequeñísimas esferas cargadas que daban vueltas en torno al núcleo, para dar paso a ver los electrones como una función de onda, y añadiéndonos un útil concepto, el de orbital.Actualmente cuando se necesita una precisión alta en cuanto a niveles de energía se refiere, se usa un modelo similar al de Schrödinger, modificando la descripción del electrón usando la ecuación relativista de Dirac, en vez de la famosa ecuación del físico austríaco. También es un modelo válido para explicar las configuraciones electrónicas de los átomos.El nombre de modelo atómico de Schrödinger, suele llevar confusión, debido a que no explica totalmente la estructura del átomo. Este modelo explica solamente la estructura electrónica del átomo y su interacción con la estructura de otros átomos, pero en ningún momento nombra al núcleo, ni hace referencia a la estabilidad de éste.
- A continuación les dejamos un vídeo para que comprendan mas el tema...Esperamos que sea de su agrado.

